KONSEP KESEIMBANGAN STRUKTUR BANGUNAN

Baca Juga:

Konsep keseimbangan struktural pada bangunan sangat penting untuk menjamin stabilitas dan keamanan. Ini melibatkan pemahaman distribusi gaya dan beban dalam suatu struktur untuk menjaga keseimbangan.

Poin Penting:  

Konsep keseimbangan struktur pada bangunan didasarkan pada keseimbangan gaya dan beban di dalam struktur untuk menjamin stabilitas dan keamanan. Konsep ini penting dalam perancangan dan konstruksi berbagai jenis bangunan dan struktur, termasuk desain arsitektur tradisional dan modern.

Apa Itu Kesetimbangan Benda Tegar?

Kesetimbangan benda tegar adalah kondisi di mana sebuah benda tetap dalam posisi diam atau bergerak dengan kecepatan konstan tanpa mengalami rotasi atau translasi. Dalam fisika, “tegar” mengacu pada sifat suatu benda untuk tetap dalam keadaan tertentu ketika dikenai gaya. Kesetimbangan benda tegar berhubungan dengan hukum Newton dan momen inersia.

Ada dua jenis kesetimbangan benda tegar:

1. Kesetimbangan Statis

   Kesetimbangan statis terjadi ketika benda berada dalam keadaan diam dan tidak bergerak. Ini berarti bahwa jumlah gaya pada benda dalam arah horizontal dan vertikal adalah nol. Artinya, hasil dari gaya-gaya yang bekerja pada benda adalah nol, sehingga benda tetap dalam posisi diam tanpa bergerak.

2. Kesetimbangan Dinamis

   Kesetimbangan dinamis terjadi ketika benda bergerak dengan kecepatan konstan tanpa mengalami percepatan. Dalam kondisi ini, gaya-gaya pada benda mungkin tidak nol, tetapi jumlah dari gaya-gaya tersebut menyebabkan benda bergerak dengan kecepatan konstan dalam garis lurus, atau dalam gerakan melingkar konstan tanpa mengalami rotasi tambahan.

Rumus Kesetimbangan Benda Tegar

Dalam fisika, untuk menganalisis kesetimbangan benda tegar, digunakan dua konsep dasar: momen gaya (torsi) dan momen inersia. Momem gaya adalah hasil perkalian antara gaya yang bekerja pada benda dengan lengan gaya (jarak dari sumbu rotasi ke titik aplikasi gaya). Momen inersia adalah besaran yang menunjukkan sejauh mana benda menghendaki untuk tetap dalam keadaan diam atau bergerak dengan kecepatan angular yang konstan.

Rumus-rumus utama yang terlibat dalam analisis kesetimbangan benda tegar adalah sebagai berikut:

Momen Gaya (τ):

Momen gaya dihitung dengan mengalikan besar gaya (F) dengan lengan gaya (d) yang diukur tegak lurus terhadap garis aksi gaya dari sumbu rotasi.
τ = F * d

Momen Inersia (I):

Momen inersia mengukur sejauh mana benda cenderung untuk tetap dalam keadaan diam atau bergerak dengan kecepatan angular konstan. Nilai momen inersia bergantung pada distribusi massa benda dan sumbu rotasi.
Untuk benda tegar sederhana seperti lingkaran atau silinder yang berputar mengelilingi sumbu tengahnya, momen inersia dihitung dengan rumus berikut:
I = (1/2) * m * r^2
(m adalah massa benda dan r adalah jari-jari dari lingkaran atau silinder)

Untuk bentuk benda lainnya atau kombinasi dari beberapa bentuk, momen inersia dapat dihitung dengan menggunakan integral.

Persamaan Kesetimbangan:
Dalam keadaan kesetimbangan, jumlah momen gaya yang bekerja pada benda harus nol terhadap sumbu rotasi tertentu. Ini dapat ditulis sebagai:
Στ = 0
(Στ adalah jumlah dari semua momen gaya)

Persamaan kesetimbangan ini membantu untuk menemukan keadaan kesetimbangan suatu benda tegar, baik dalam keadaan diam maupun bergerak dengan kecepatan angular konstan.

Contoh Soal Kesetimbangan Benda Tegar

Contoh Soal:

Sebuah papan sepanjang 2 meter diletakkan di atas dua penyangga di kedua ujungnya. Penyangga kiri berada pada jarak 0,5 meter dari ujung kiri papan, sedangkan penyangga kanan berada pada jarak 0,8 meter dari ujung kanan papan. Sebuah balok dengan massa 5 kg diletakkan pada papan pada jarak 1,2 meter dari ujung kiri papan. Tentukan berapa besar massa dari balok kedua agar papan tetap dalam kesetimbangan.

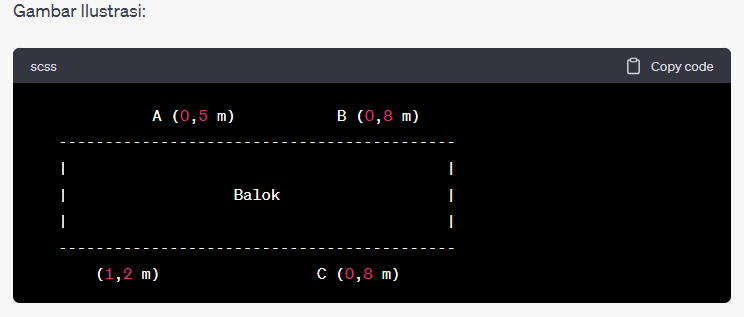
Catatan: A, B, dan C adalah titik-titik di mana penyangga ditempatkan pada papan. A adalah penyangga kiri, B adalah penyangga kanan, dan C adalah posisi balok diletakkan pada papan.

Langkah penyelesaian:

1. Identifikasi gaya-gaya yang bekerja pada papan dan balok:
   Gaya berat balok mengarah ke bawah dengan besar m * g, di mana m adalah massa balok (yang akan kita cari) dan g adalah percepatan gravitasi.
   Gaya berat papan mengarah ke bawah dengan besar m_papan * g, di mana m_papan adalah massa papan. Untuk kesederhanaan, asumsikan massa papan sangat besar sehingga perhatikan bahwa gaya berat papan akan memiliki momen nol terhadap titik-titik penyangga.
   Gaya penyangga di A (F_A) dan B (F_B) mengarah ke atas untuk menyeimbangkan gaya berat balok dan papan.
   
2. Tentukan momen gaya yang bekerja pada papan terhadap titik penyangga:
   Momen gaya di A: F_A * 0,5 m (karena jarak dari penyangga A ke ujung kiri papan adalah 0,5 m).
   Momen gaya di B: F_B * 0,8 m (karena jarak dari penyangga B ke ujung kanan papan adalah 0,8 m).
   
3. Terapkan persamaan kesetimbangan untuk momen gaya:
   Dalam keadaan kesetimbangan, total momen gaya harus nol, sehingga:
   Στ = 0
   F_A * 0,5 m – F_B * 0,8 m = 0
   
4. Tentukan besar gaya di A dan B:
   Karena papan tetap dalam kesetimbangan, maka F_A = F_B.
   
5. Tentukan besar gaya penyangga F_A:
   F_A = (m * g) + (m_papan * g)
   F_A = (m * g) + (m_papan * g)
   
6. Tentukan momen gaya berat balok terhadap titik penyangga:
   Momen gaya berat balok di C: (m * g) * 1,2 m
   
7. Terapkan persamaan kesetimbangan untuk momen gaya:
   Dalam keadaan kesetimbangan, total momen gaya harus nol, sehingga:
   F_A * 0,5 m – F_B * 0,8 m – (m * g) * 1,2 m = 0
   
8. Tentukan besar gaya di A dan B:
   F_A = (m * g) + (m_papan * g)
   
9. Tentukan momen gaya berat balok terhadap titik penyangga:
   Momen gaya berat balok di C: (m * g) * 1,2 m
   
10. Terapkan persamaan kesetimbangan untuk momen gaya:
    Dalam keadaan kesetimbangan, total momen gaya harus nol, sehingga:
    F_A * 0,5 m – F_B * 0,8 m – (m * g) * 1,2 m = 0
    
11. Tentukan besar gaya penyangga F_A:
    F_A = (m * g) + (m_papan * g)
    
12. Tentukan momen gaya berat balok terhadap titik penyangga:
    Momen gaya berat balok di C: (m * g) * 1,2 m
    
13. Terapkan persamaan kesetimbangan untuk momen gaya:
    Dalam keadaan kesetimbangan, total momen gaya harus nol, sehingga:
    F_A * 0,5 m – F_B * 0,8 m – (m * g) * 1,2 m = 0
    
14. Gantikan F_A dengan (m * g) + (m_papan * g) dalam persamaan di atas:
    ((m * g) + (m_papan * g)) * 0,5 m – F_B * 0,8 m – (m * g) * 1,2 m = 0
    
15. Atur ulang persamaan di atas untuk mencari F_B:
    F_B * 0,8 m = ((m * g) + (m_papan * g)) * 0,5 m – (m * g) * 1,2 m
    F_B = (((m * g) + (m_papan * g)) * 0,5 m – (m * g) * 1,2 m) / 0,8 m
    
16. Tentukan nilai F_B dalam persamaan di atas untuk memperoleh nilai massa balok (m):
    m * g = (((m * g) + (m_papan * g)) * 0,5 m – (m * g) * 1,2 m) / 0,8 m
    
17. Cari nilai m:
    m = (((m * g) + (m_papan * g)) * 0,5 m – (m * g) * 1,2 m) / (0,8 m * g)
    
18. Sederhanakan persamaan di atas untuk mencari nilai m:
    m = (0,5 – 1,2) / 0,8
    m = -0,7 / 0,8
    m = -0,875 kg

Penerapan Kesetimbangan Benda Tegar

Penerapan kesetimbangan benda tegar banyak terjadi dalam berbagai situasi dalam kehidupan sehari-hari dan dalam berbagai industri. Beberapa contoh penerapannya antara lain:

1. Bangunan dan Konstruksi:

   Kesetimbangan benda tegar sangat penting dalam perancangan bangunan dan struktur. Ketika merancang bangunan seperti jembatan, gedung, atau menara, insinyur harus memastikan bahwa struktur tersebut dalam kesetimbangan agar dapat menahan beban yang diberikan kepadanya. Analisis kesetimbangan benda tegar membantu mengidentifikasi titik-titik di mana beban didistribusikan secara merata dan aman.

2. Kendaraan dan Transportasi:

   Kesetimbangan benda tegar juga relevan dalam desain kendaraan. Ketika merancang kendaraan seperti mobil, pesawat, atau kapal, penting untuk memastikan kesetimbangannya agar kendaraan dapat beroperasi secara stabil dan aman. Analisis kesetimbangan juga membantu dalam mendistribusikan muatan secara tepat di dalam kendaraan.

3. Fisika dalam Kehidupan Sehari-hari:

   Dalam kehidupan sehari-hari, kesetimbangan benda tegar berlaku pada objek-objek yang diam seperti meja, kursi, atau rak. Objek-objek ini tetap dalam kesetimbangan statis karena gaya-gaya yang bekerja pada benda seimbang.

4. Pada Ayunan:

   Ayunan seperti gantungan dan jungkat-jungkit menggunakan prinsip kesetimbangan benda tegar untuk memastikan ayunan bergerak secara aman dan stabil.

5. Penerapan dalam Mekanika Mesin:

   Dalam industri dan mekanika mesin, kesetimbangan benda tegar digunakan untuk merancang dan mengatur distribusi massa pada berbagai komponen mesin seperti poros, engsel, dan benda-benda yang berputar agar mesin dapat berfungsi secara efisien dan aman.

6. Perangkat Elektronik:

   Pada perangkat elektronik seperti ponsel cerdas dan laptop, kesetimbangan benda tegar digunakan dalam desain mekanik dan posisi baterai untuk menjaga keseimbangan dan mencegah perangkat dari goyang atau bergerak dengan tidak stabil.

7. Falsafah Hidup (dalam kehidupan manusia)

   Dalam kehidupan makhluk hidup dan lingkungan, konsep kesetimbangan hidup dalam berbagai falsafah kehidupan manusia menekankan pentingnya hubungan harmonis antara manusia, alam, dan Tuhan untuk mencapai kebahagiaan dan keharmonisan dalam kehidupannya.

Konsep kesetimbangan hidup juga terdapat dalam ajaran Jawa, seperti dalam konsep Hamemayu Hayuning Bawana. Konsep ini menekankan keseimbangan kehidupan antara manusia dengan manusia, manusia dengan alam, dan manusia dalam hubungannya dengan Tuhan. Masyarakat Jawa dalam melaksanakan kehidupan sehari-hari masih memegang kuat prinsip hidup yang berhubungan dengan menjaga keseimbangan antara kehidupan alam dan manusia

Hamemayu hayuning bawana bermakna memperindah keindahan dunia. Memayu hayuning bawana adalah ihwal space culture atau ruang budaya sekaligus spiritual culture atau spiritualitas budaya. Memayu hayuning bawana memang upaya melindungi keselamatan dunia baik lahir maupun batin. Orang Jawa merasa berkewajiban untuk memayu hayuning bawana atau memperindah keindahan dunia, hanya inilah yang memberi arti dari hidup. Di satu fisik secara harafiah, manusia harus memelihara dan memperbaiki lingkungan fisiknya. Sedangkan di pihak lain secara abstrak, manusia juga harus memelihara dan memperbaiki lingkungan spritualnya. (Suwardi Endraswara, 2013).

Penutup

Sekian Penjelasan Singkat Mengenai KONSEP KESEIMBANGAN STRUKTUR BANGUNAN. Semoga Bisa Menambah Pengetahuan Kita Semua.

Apa reaksimu setelah membaca KONSEP KESEIMBANGAN STRUKTUR BANGUNAN